Shop Solver

Compound Angle Calculator

Command path:  Tools->Compound Angle
This tool calculates the rotation and tilt angles required to mill a flat facet or drill a hole on a compound angle.

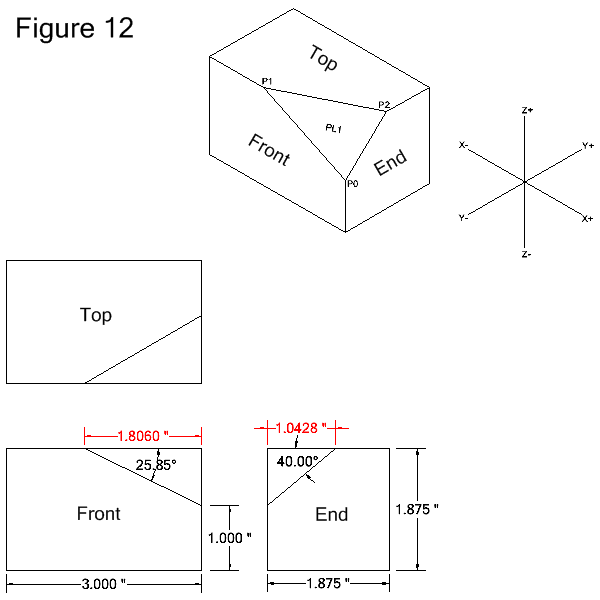
The following 3 examples for milling a compound facet refer to Figure 12 below.  All given dimensions are shown in black.  Calculated dimensions are shown in red.  The examples assume that the facet will be milled with the bottom of the cutter.  Click here for an example for drilling a hole on a compound angle.

Note:  The Triangle Solver tool can be used to determine the calculated dimensions shown in Figure 12.

Example for milling a compound facet via a plane definition
Example for milling a compound facet via the definitions of 3 points
Example for milling a compound facet via the definitions of 2 vectors






Example 1: Milling a Facet via a Plane Definition



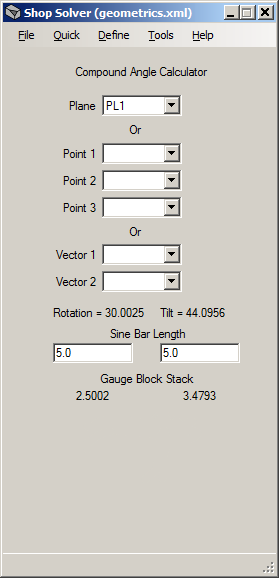
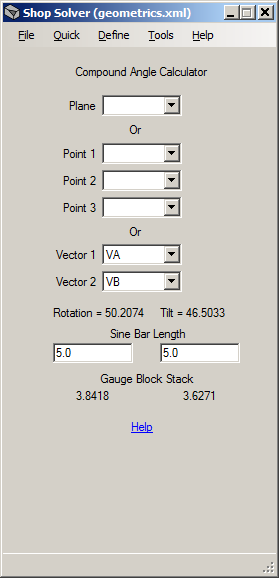
In the tool image above the plane PL1 has been selected in the Plane  drop-down list.  Click here for the plane definition descriptions.  In this example the plane was defined as going through 3 nonlinear points.  Figure 12 above shows the 3 points named P0, P1 and P2.  For reference the coordinates of the 3 points are:

P0 = X0 Y0 Z0
P1 = X-1.806 Y0 Z0.875
P2 = X0 Y1.0428 Z0.875

Selecting the plane automatically calculates the rotation and tilt angles required to mill the facet.  The angles are in degrees and are shown below the Vector  drop-down fields (see Note 1).

Gauge block stacks for the rotation and tilt angles may be determined by entering the lengths of the sine bars to be used.  In the tool image sine bar lengths of 5.0 were specified.


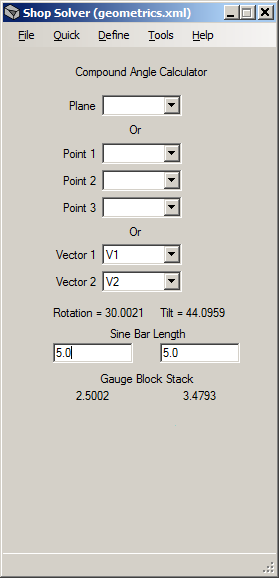
Example 2: Milling a Facet via 3 Point Defintions



In the tool image above 3 points have been selected, each representing a corner of the facet to be milled.  Click here for the point definition descriptions.  Figure 12 above shows the 3 points named P0, P1 and P2.  For reference the coordinates of the 3 points are:

P0 = X0 Y0 Z0
P1 = X-1.806 Y0 Z0.875
P2 = X0 Y1.0428 Z0.875

When all 3 points have been selected the tool automatically calculates the rotation and tilt angles required to mill the facet.  The angles are in degrees and are shown below the Vector  drop-down fields (see Note 1).

Gauge block stacks for the rotation and tilt angles may be determined by entering the lengths of the sine bars to be used.  In the tool image sine bar lengths of 5.0 were specified.



Example 3: Milling a Facet via 2 Vector Defintions



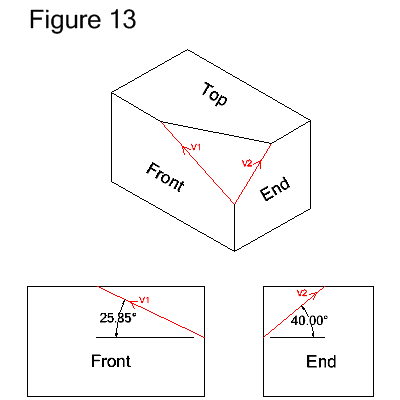
In the tool image above, 2 vectors have been selected.  Click here for the vector definition descriptions.  Each vector represents an edge on the facet.  Figure 13 below shows the 2 vectors, named V1 and V2, in red.  The vectors are defined as "Length (Magnitude) and an Angle in a Plane".  For reference the vector definitions are:

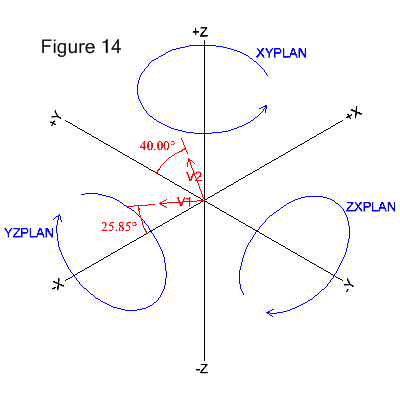
V1=VECTOR/LENGTH,1.0,ATANGL,25.85,ZXPLAN
V2=VECTOR/LENGTH,1.0,ATANGL,40.0,YZPLAN

The vector properties are:
Note:  Any 2 edges of the facet may be used.  For example:

V3=VECTOR/LENGTH,1.0,ATANGL,-154.15,ZXPLAN  $$ complement of angle of V1 (front view)
V4=VECTOR/LENGTH,1.0,ATANGL,30.0,XYPLAN  $$ angle when looking down at top view





Figure 14 below depicts another representation of vectors V1 and V2.  The blue circles show the direction of positive angles around their respective axes.  Positive angles are counter-clockwise and determined by looking along an axis from the positive end toward the origin.  Zero degrees is at 3 o'clock when looking along an axis.



When both vectors have been selected the tool automatically calculates the rotation and tilt angles required to mill the facet.  The angles are in degrees and are shown below the Vector  drop-down fields (see Note 1).

Gauge block stacks for the rotation and tilt angles may be determined by entering the lengths of the sine bars to be used.  In the tool image sine bar lengths of 5.0 were specified.


Example 4: Drilling a Hole via 2 Vector Definitions



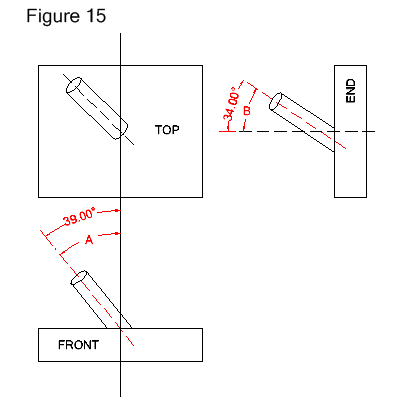
In the tool image above, 2 vectors have been selected.  The vectors represent the angles of a cylinder's centerline, as shown in Figure 15 below.  (Click here for the vector definition descriptions.)  The vectors, named VA and VB, are associated with angles "A" and "B".  The vectors' angles are those required to rotate the cylinder into a vertical position.  Note:  The angles are not the compound angles required to drill the hole, just the values given on the print or in the specification.

In Figure 15 below, VA must be rotated 39.0 degrees in the ZX plane to become vertical.  VB must be rotated 34.0 degrees in the YZ plane to become vertical.  Refer to Figure 14 above for how to determine direction of rotation.  Both vectors are defined as "Length (Magnitude) and an Angle in a Plane".  For reference the vector definitions are:

VA=VECTOR/LENGTH,1.0,ATANGL,39.0,ZXPLAN
VB=VECTOR/LENGTH,1.0,ATANGL,34.0,YZPLAN

The vector properties are:



When both vectors have been selected the tool automatically calculates the rotation and tilt angles required to drill the hole.  The angles are in degrees and are shown below the Vector  drop-down fields (see Note 1).

Gauge block stacks for the rotation and tilt angles may be determined by entering the lengths of the sine bars to be used.  In the tool image sine bar lengths of 5.0 were specified.


Note 1
Depending upon the set-up, it may be necessary to calculate and use the complement of an angle, especially if the required sine bar angle is greater than 45 degrees.  This is because the gauge block stack required to obtain the angle may be too great for setting the sine bar.  Therefore the angle of the sine bar and the part surface contacting the sine bar must be altered.  An example is shown below.  On the left the part to be milled is resting on its narrow width causing the angle of the sine bar to be too steep. On the right the part is resting on its length and the angle of the sine bar is acceptable.  Again, depending upon the set-up, this may need to be applied to either the tilt or rotation angle.