Shop Solver
For instructions on how to use the Define Commands, please click here.
Define Plane
A plane is a
flat 2-dimensional surface that extends infinitely far in all
directions parallel with the plane. A plane may be defined by any
of the following:
By Coefficients
Through 3 Non-collinear Points
Through a Point and Parallel to a Plane
Parallel to a Plane at a Distance
Through a Point and Perpendicular to a Vector
Through 2 Points and Perpendicular to a Plane
Through a Point and Perpendicular to 2 Intersecting Planes
Through a Point and Tangent to a Cylinder
By Coefficients
PLANE/a,b,c,d
The parameters are the coefficients of the plane equation ax + by + cz = d
where a, b and c define the head of a vector that is normal to
the plane and whose foot is at the origin. "d" is the
perpendicular distance from the origin to the plane multiplied by the
length of the vector. When the vector is a
unit vector (i.e. a vector of length 1.0) the value of d is simply the
perpendicular distance from the origin to the plane. Otherwise d
must be scaled to attain the desired distance from the origin.
In
figure Plane.1 below, PL1 is a plane parallel to the XY plane at Z=4.0.
Setting a, b and c to define the unit vector 0,0,1 requires that
d be 4.0 in order to scale the vector to a length of 4.0.
PL2
is a plane tilted on a 45 degree angle to the ZX plane and has a
perpendicular distance of 5.0 from the origin. Setting a, b and c
to 0,3,3 (which is NOT a unit vector) requires that d be the desired
perpendicular distance of 5.0 scaled by the length of the vector
(4.24264). The math follows:
Length of the vector normal to PL2 = SQRT(0² + 3² + 3²) = 4.24264
The desired perpendicular distance from the origin to PL2 is 5.0 so d = 5 * 4.24264 = 21.2132.
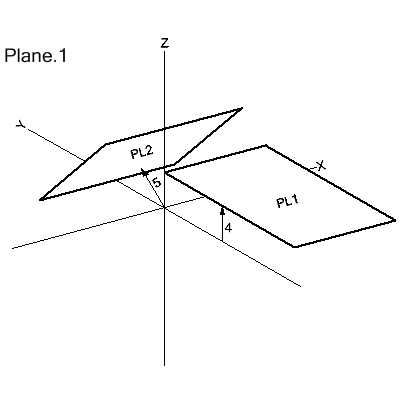
PL1=PLANE/0,0,1.0,4.0
PL2=PLANE/0,3.0,3.0,21.2132
Through 3 Non-collinear Points
PLANE/point1,point2,point3
The plane is defined as passing through 3 non-collinear (not all on the same line) points.
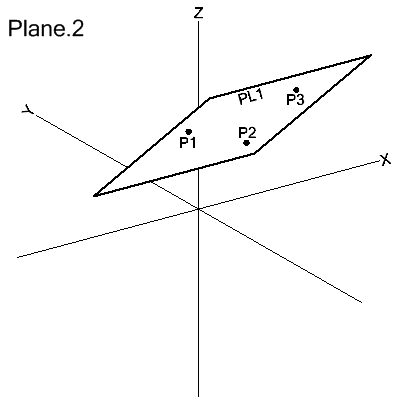
PL1=PLANE/P1,P2,P3
Through a Point and Parallel to a Plane
PLANE/point,PARLEL,plane
The plane is defined as passing through point and parallel to plane.
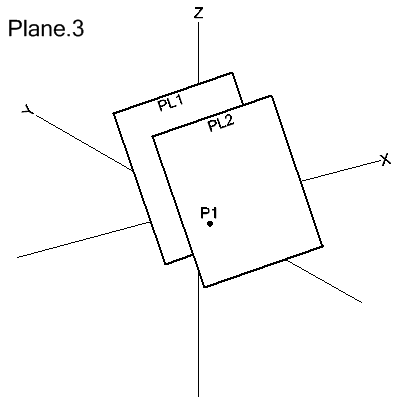
PL2=PLANE/P1,PARLEL,PL1
Parallel to a Plane at a Distance
PLANE/PARLEL,plane,modifier,distance
modifier: XLARGE | XSMALL | YLARGE | YSMALL | ZLARGE | ZSMALL
The
plane is defined as parallel to plane. The 2 planes are
offset from each other by the given perpendicular distance.
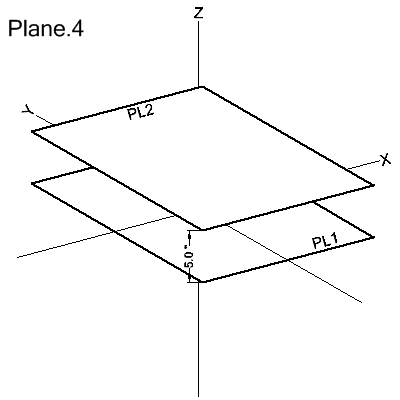
PL2=PLANE/PARLEL,PL1,ZLARGE,5.0
The directional modifiers are defined here.
Through a Point and Perpendicular to a Vector
PLANE/point,PERPTO,vector
The plane is defined as passing through point and is positioned such that it is perpendicular to the given vector.
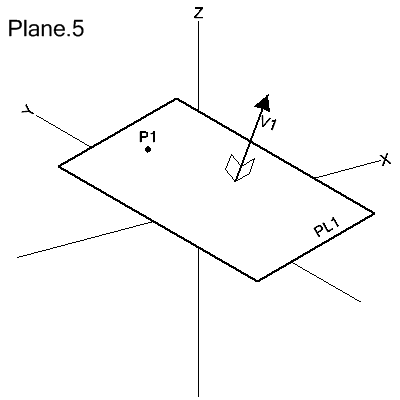
PL1=PLANE/P1,PERPTO,V1
Through 2 Points and Perpendicular to a Plane
PLANE/point1,point2,PERPTO,plane
The
plane is defined as passing through point1 and point2 and is perpendicular to
the given plane. A line passing through the 2 points must not be
perpendicular to the given plane.
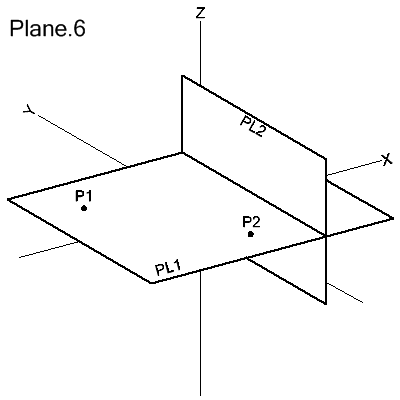
PL1=PLANE/P1,P2,PERPTO,PL2
Through a Point and Perpendicular to 2 Intersecting Planes
PLANE/point,PERPTO,plane1,plane2
The plane is defined as passing through point and is perpendicular to both plane1 and plane2.
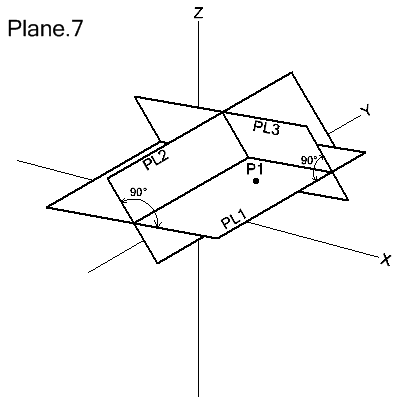
PL1=PLANE/P1,PERPTO,PL2,PL3
Through a Point and Tangent to a Cylinder
PLANE/point,modifier,TANTO,cylinder
modifier: XLARGE | XSMALL | YLARGE | YSMALL | ZLARGE | ZSMALL
The plane is defined as passing through point and tangent to cylinder. The modifier defines which of 2 possible planes is desired by comparing their points of tangency with cylinder.
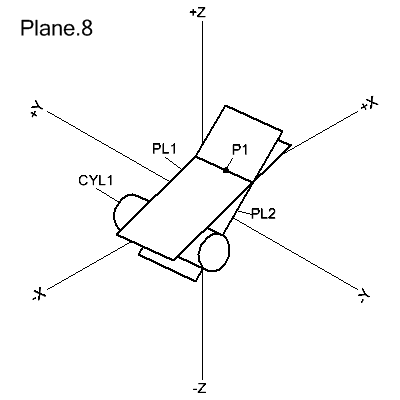
PL1=PLANE/P1,ZLARGE,TANTO,CYL1
PL2=PLANE/P1,ZSMALL,TANTO,CYL1
The directional modifiers are defined here.







