Shop Solver

For instructions on how to use the Define Commands, please click here.

Define Vector

A vector is a line segment that has both magnitude (length) and direction.  It is has a starting point known as the foot and an ending point known as the head.  The direction of the vector extends from the foot to the head.  The magnitude of the vector is the distance between the foot and the head and is always positive.  All vectors with the same magnitude and direction are treated as equivalent no matter where their feet and heads are defined.  When not specified in a definition the foot defaults to the origin.  In many cases a vector definition may substitute a given vector with a point definition.  If a point is specified then it is assumed to be a vector whose foot is the origin.  A vector may be defined by any of the following:

Rectangular Coordinates
2 End Points (X1, Y1, Z1, X2, Y2,Z2)
2 End Points (Point1, Point2)
Perpendicular to a Plane
Scalar Times a Vector
Scalar Times a Point
Cross Product of 2 Vectors or Points
Normalizing a Vector by Components
Normalizing a Vector by a Vector
Normalizing a Vector by a Point
Length (Magnitude) and an Angle in a Plane
Parallel to the Intersection of 2 Planes
Addition or Subtraction of 2 Vectors or Points
In the XY Plane Having an Angle with a Line



Rectangular Coordinates

VECTOR/dx,dy,dz
The vector is defined by the components dx, dy, dz.  The components are the distances along the X-, Y- and Z-axes respectively.  This definition is equivalent to the 2 End Points definitions below when X1=0, Y1=0 and Z1=0, or when the X, Y and Z distances from Point2  to Point1  is equal to dx, dy and dz.  See figure Vector.1 below.


2 End Points (X1, Y1, Z1, X2, Y2,Z2)
2 End Points (Point1, Point2)

VECTOR/x1,y1,z1,x2,y2,z2
VECTOR/point1,point2
The vector is defined by coordinates of its foot and head.  In the former the foot is at x1, y1, z1 and the head is at x2, y2, z2.  In the latter the foot is at point1 and the head is at point2.  


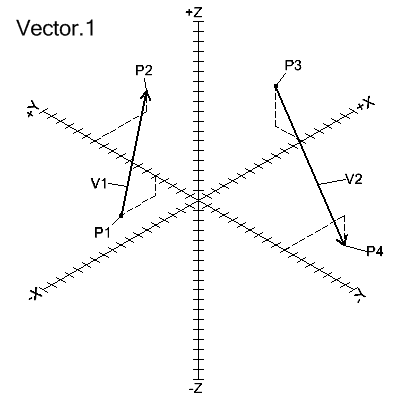
V1=VECTOR/10,7,4
V2=VECTOR/-5,-13,-7
                  or
V1=VECTOR/-4,5,-2,6,12,2
V2=VECTOR/12,3,4,7,-10,-3
                  or
V1=VECTOR/P1,P2
V2=VECTOR/P3,P4


Perpendicular to a Plane

VECTOR/PERPTO,plane,modifier
modifier: NEGX | NEGY | NEGZ | POSX | POSY | POSZ
The vector is defined as perpendicular to plane.  The modifier indicates the direction of the vector.  NEGX indicates that the vector points in the negative X direction, POSZ in the positive Z direction, etc.


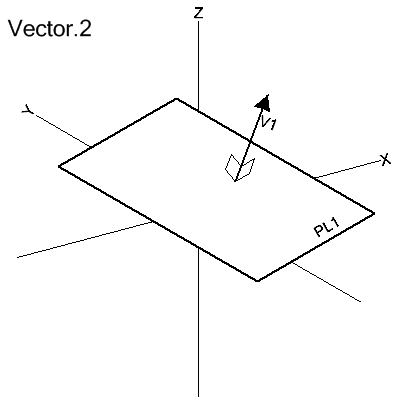
V1=VECTOR/PERPTO,PL1,POSZ


Scalar Times a Vector
Scalar Times a Point

VECTOR/scalar,TIMES,vector
VECTOR/scalar,TIMES,point
The defined vector is formed by multiplying each component of vector by scalar.  If point is specified then the X, Y and Z coordinates of point are multiplied by scalar.


V2=VECTOR/3.25,TIMES,V1
V4=VECTOR/2.4,TIMES,V3
V5=VECTOR/-2.6,TIMES,P1


Cross Product of 2 Vectors or Points

VECTOR/vector1 | point1, CROSS, vector2 | point2
The vector is defined as the cross product of vector1 (or point1) with vector2 (or point2).  If points are specified then they are assumed to be vectors whose feet are the origin.

The cross product of 2 vectors is a third vector that is perpendicular to the plane formed by the 2 given vectors.  The length of the resultant vector is the length of vector1  times the length of vector2  times the sine of the angle formed between the 2 given vectors.  Its direction is determined according to the right-hand rule.


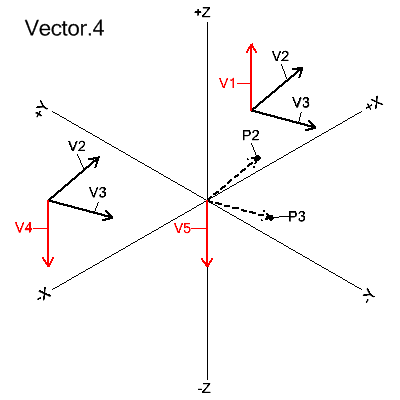
V1=VECTOR/V3,CROSS,V2
V4=VECTOR/V2,CROSS,V3
V5=VECTOR/P2,CROSS,P3


Normalizing a Vector by Components
Normalizing a Vector by a Vector
Normalizing a Vector by a Point

VECTOR/UNIT,x,y,z
VECTOR/UNIT,vector
VECTOR/UNIT,point
The vector is defined by normalizing the given vector.  The given vector may be specified by the coordinates of its head, by another vector, or a point.  If the given vector is specified by coordinates then its foot is assumed to be the origin.  It the given vector is specified by a point then the point is assumed to be a vector with its foot at the origin.

A normalized or unit vector is one that has the same direction as the given vector but with a length of 1.


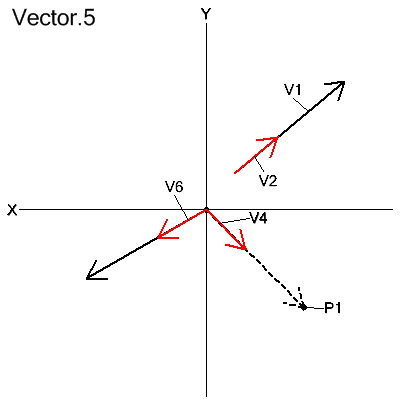
V2=VECTOR/UNIT,V1
V4=VECTOR/UNIT,P1
V6=VECTOR/UNIT,-10.4,-6.2,0


Length (Magnitude) and an Angle in a Plane

VECTOR/LENGTH,len,ATANGL,theta,modifier
modifier: XYPLAN | YZPLAN | ZXPLAN
The vector is defined as having length len and at angle theta in the given plane.  The angle is measured from the positive axis belonging to the first letter of the plane modifier.  Note that rotation occurs around the axis component missing from the plane.  For example, XYPLAN is missing the Z-component so rotation occurs around the Z-axis.


V1=VECTOR/LENGTH,10,ATANGL,315,XYPLAN
V2=VECTOR/LENGTH,4,ATANGL,60,YZPLAN
V3=VECTOR/LENGTH,7,ATANGL,150,ZXPLAN
                                        or
V1=VECTOR/LENGTH,10,ATANGL,-45,XYPLAN
V2=VECTOR/LENGTH,4,ATANGL,-300,YZPLAN
V3=VECTOR/LENGTH,7,ATANGL,-210,ZXPLAN


Parallel to the Intersection of 2 Planes

VECTOR/PARLEL,INTOF,plane1,plane2,modifier
modifier: NEGX | NEGY | NEGZ | POSX | POSY | POSZ
The vector is defined as parallel to the line of intersection of plane1 with plane2.  Its direction is determined by modifier according to the positive or negative axis component of modifier when applied to the X, Y or Z coordinates of the vector's head.  For example, POSZ specifies a positive Z-component.

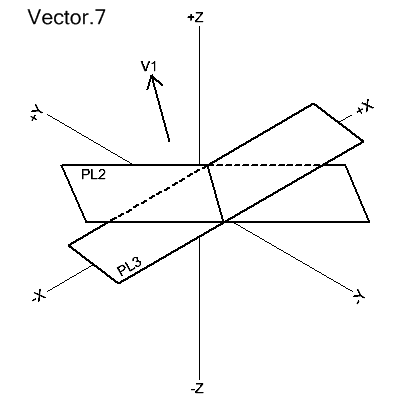
V1=VECTOR/PARLEL,INTOF,PL2,PL3,POSY


Addition or Subtraction of 2 Vectors or Points

VECTOR/vector1 | point1, operator, vector2 | point2
operator: PLUS | MINUS
The vector is defined by the addition or subtraction of vector1 (or point1) with vector2 (or point2).  If points are specified then they are assumed to be vectors whose feet are the origin.


P1=POINT/1.0,2.0,3.0
P2=POINT/10.0,5.0,6.0
V3=VECTOR/P1,PLUS,P2
V4=VECTOR/3.0,-9.0,0,7.0,-3.0,0
V5=VECTOR/8.0,-14.0,0,3.0,-9.0,0
V6=VECTOR/V4,PLUS,V5
V7=VECTOR/-9.0,8.0,0,-5.0,14.0,0
V8=VECTOR/-9.0,8.0,0,-4.0,3.0,0
V9=VECTOR/V7,MINUS,V8


In the XY Plane Having an Angle with a Line

VECTOR/ATANGL,theta,line,modifier
modifier: POSX | XLARGE | POSY | YLARGE | NEGX | XSMALL | NEGY | YSMALL
The vector is defined as a unit vector at angle theta to line.  The modifier specifies which of the 2 possible vectors is required.  POSX and XLARGE have the same meaning and select the vector whose head has a positive X-component.  The other pairs of modifiers apply similar logic.


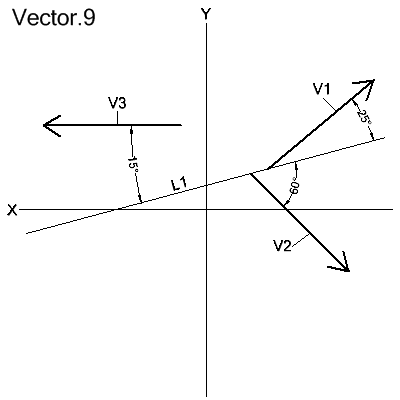
V1=VECTOR/ATANGL,25.0,L1,POSX
V2=VECTOR/ATANGL,-60.0,L1,POSX
V3=VECTOR/ATANGL,-15.0,L1,XSMALL