Shop Solver

Circle/Circle Tool

Command path:  Quick->Circle/Circle
The purpose of this tool is to determine the intersection points of two circles, if any.  

Quick Start

The tool is two-dimensional (2D).  The circles must lie in the same plane and the plane must be parallel with the XY plane.

To find the intersection points of two circles:
1)  In the boxes labeled "Circle 1" and "Circle 2", enter the X and Y values of the circles' center points and their radii.
2)  Click the Calculate  button.  If the button is disabled then tab to or click on another field (such as the Offset  field).  The points of intersection are shown in the fields above the button.  Note:  If the circles are tangent to each other then the points of intersection will be the same.

For information about the Offset  fields click here.


Overview

The application window is divided into three sections.  The upper two sections are for defining the two circles.  The lower section displays the results of the intersection calculation.  The buttons in the lower section are described below.


Image CircleCircle



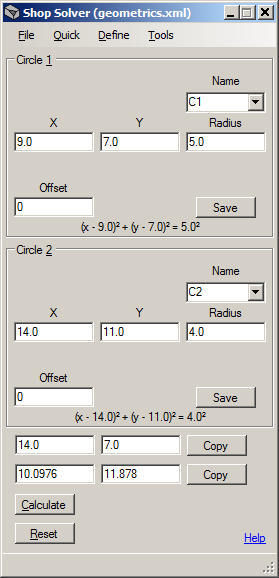
Referring to Image CircleCircle above, a circle is defined as having a center point at X and Y and a radius.

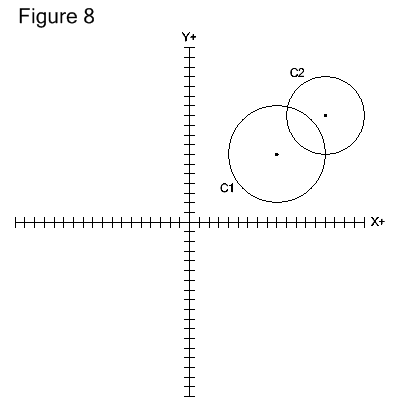
Figure 8 shows two circles that intersect.  Circle C1 has X9.0, Y7.0 as its center point and a radius of 5.0.  Circle C2 has X14.0, Y11.0 as its center point and a radius of 4.0.  The circles are shown entered into their respective definition sections in image CircleCircle above.





The bottom section of Image CircleCircle shows the points of intersection of circles C1 and C2 after the Calculate  button was clicked.  The Copy  buttons, when clicked, copy the X and Y values of their respective points of intersection to the clipboard.  The Reset  button clears all fields in the window.

The Name  fields are used in conjunction with the Save  buttons.  When a name is specified the Save  button stores the circle definition in memory.  A definition may be recalled later by selecting the name from the Name field's drop down list.  Saving a definition in memory is optional and is not required for calculating intersections.  If not saved to a file, all definitions saved in memory are lost when Shop Solver is closed.  See the File command for saving and loading definitions to and from a file.

A Point definition may be created by right-clicking with the mouse on any of the X fields.  A pop-up menu will appear with a Create Point  command.  The command will take you to the point definition tool and the X, Y, and Z (Z when applicable) values will be automatically entered into the proper fields.  For more about point definitions click here.

If any points have been saved in memory then their X and Y values may be automatically pasted into the circle definition fields.  Right-click on any X field in the definition sections and a pop-up menu will appear with the names of all points currently saved in memory.  Select a point to paste its X and Y values into the fields.

All numeric entry fields in Shop Solver can evaluate and solve mathematical expressions.  You may enter expressions using the common arithmetic operators +, -, *, /, (, ), %, and ^.  In addition 30+ functions are supported such as trigonometric functions, common math functions (square and cube roots, absolute values, min/max, etc.) and common shop functions such as surface feet per minute (SFM) to RPM, inch to millimeter, and others.  Expressions are evaluated when an entry field loses the focus by tabbing to or clicking on something else.  For a full description of this feature click here.

Offsets

The usage of the Offset  field for a circle is depicted in Figure 7.  The outline of a simple part is shown in black and the paths of a 0.5" end mill around the inside and the outside of the part are shown in blue and green respectively.

The sign of the offset (+/-) determines its direction.  A positive offset increases the circle's radius during the intersection calculation.  A negative offset decreases the radius.