Shop Solver

For instructions on how to use the Define Commands, please click here.

Define Circle

A circle is the set of all points in a plane that are equidistant from a given point, the center.  The distance from the center to any point on the circle is the radius.  A circle may be defined by any of the following:

Coordinates of the Center and the Radius
Center Point and Radius
Center and a Line to Which it is Tangent
Center and a Point on the Circumference
Through 3 Points on the Circumference
Center Point and Tangent to a Circle
Radius and Tangent to 2 Intersecting Lines
Radius and Tangent to a Line and Passing Through a Point
Radius and Tangent to a Line and a Circle
Radius and Tangent to 2 Circles
Through 2 Points and the Radius
Tangent to 3 Lines
Tangent to 2 Lines and a Circle
Radius, a Point on the Circumference and Tangent to a Circle
Intersection of a Plane and a Sphere



Coordinates of the Center and the Radius

CIRCLE/x-coord,y-coord,z-coord,radius
The circle is defined with its center at the x, y, z coordinate, and by its radius.


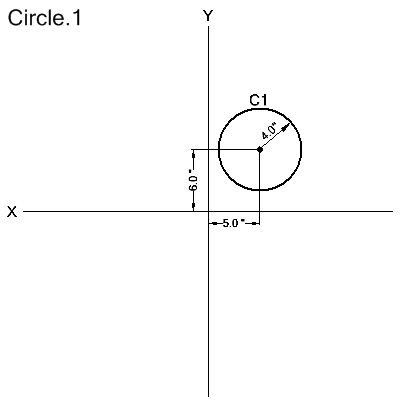
C1=CIRCLE/5.0,6.0,0,4.0


Center Point and Radius

CIRCLE/CENTER,point,RADIUS,radius
The circle is defined with its center at point, and by its radius.


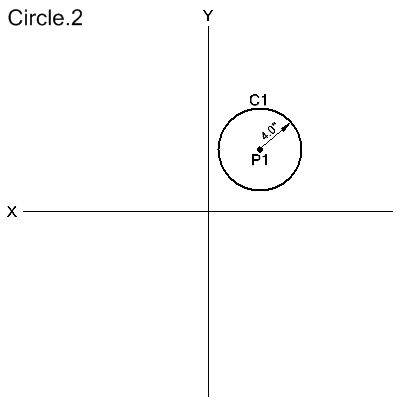
C1=CIRCLE/CENTER,P1,RADIUS,4.0


Center and a Line to Which it is Tangent

CIRCLE/CENTER,point,TANTO,line
The circle is defined with its center at point and tangent to line.


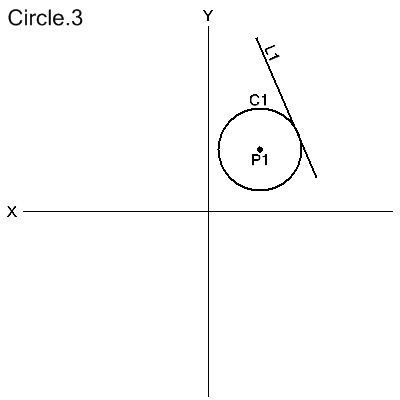
C1=CIRCLE/CENTER,P1,TANTO,L1


Center and a Point on the Circumference

CIRCLE/CENTER,point1, point2
The circle is defined with its center at point1 and passing through point2.


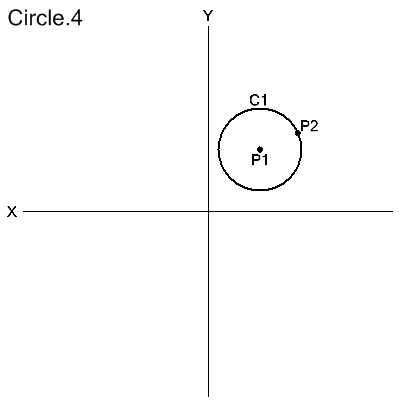
C1=CIRCLE/CENTER,P1,P2


Through 3 Points on the Circumference

CIRCLE/point1,point2,point3
The circle is defined as passing through the 3 non-collinear points point1, point2 and point3.


C1=CIRCLE/P1,P2,P3


Center Point and Tangent to a Circle

CIRCLE/CENTER,point,modifier,TANTO,circle
modifier:  LARGE | SMALL
Th circle is defined with its center at point and tangent to circle.  The modifier means that the circle being defined is either the larger or the smaller of the 2 possible solution circles, unless the given point is also the center of the given circle.  In that case the modifier is immaterial.


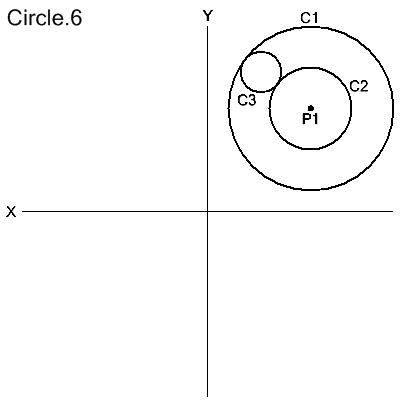
C1=CIRCLE/CENTER,P1,LARGE,TANTO,C3
C2=CIRCLE/CENTER,P1,SMALL,TANTO,C3


Radius and Tangent to 2 Intersecting Lines

CIRCLE/modifier1,line1,modifier2,line2,RADIUS,radius
modifier1: XLARGE | XSMALL | YLARGE | YSMALL
modifier2: XLARGE | XSMALL | YLARGE | YSMALL
The circle is defined as tangent to 2 lines with the given radius.  Four possible solution circles exist and the 2 modifiers define which circle is defined.  The unique solution circle whose center meets the criteria of the 2 modifiers is selected.


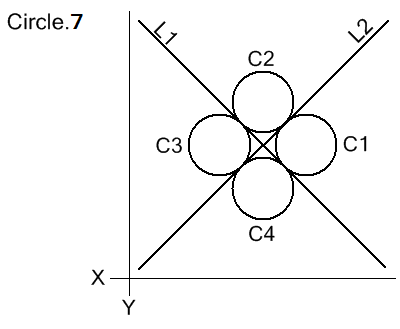
C1=CIRCLE/YLARGE,L1,YSMALL,L2,RADIUS,2.071
C2=CIRCLE/XLARGE,L1,XSMALL,L2,RADIUS,2.071
C3=CIRCLE/YSMALL,L1,YLARGE,L2,RADIUS,2.071
C4=CIRCLE/XLARGE,L2,XSMALL,L1,RADIUS,2.071

The directional modifiers are defined here.


Radius and Tangent to a Line and Passing Through a Point

CIRCLE/TANTO,line,modifier,point,RADIUS,radius
modifier: XLARGE | XSMALL | YLARGE | YSMALL
The circle is defined as tangent to line and passing through point, and with the given radius.  There are 2 possible solution circles and the modifier defines which circle's center satisfies the criteria with respect to the given point.



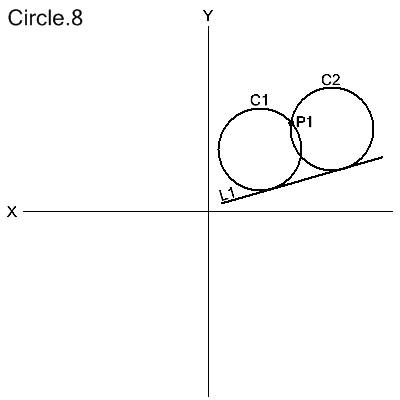
C1=CIRCLE/TANTO,L1,XSMALL,P1,RADIUS,4.0
C2=CIRCLE/TANTO,L1,XLARGE,P1,RADIUS,4.0
                                       or
C1=CIRCLE/TANTO,L1,YSMALL,P1,RADIUS,4.0
C2=CIRCLE/TANTO,L1,YLARGE,P1,RADIUS,4.0

The directional modifiers are defined here.


Radius and Tangent to a Line and a Circle

CIRCLE/modifier1,line,modifier2,modifier3,circle,RADIUS,radius
modifier1: XLARGE | XSMALL | YLARGE | YSMALL
modifier2: XLARGE | XSMALL | YLARGE | YSMALL
modifier3: IN | OUT
The defined circle is tangent to both line and circle, and with the given radius.  There are 8 possible solution circles.  Modifier1 describes where the center of the defined circle is in relation to the given line.  Modifier3 describes whether the center of the defined circle is inside or outside of the given circle.  Modifier2 selects which of the 2 final possible solution circle centers meets the criteria with respect to the center of the given circle.


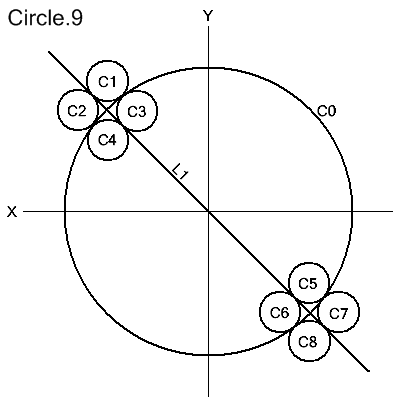
C1=CIRCLE/YLARGE,L1,XSMALL,OUT,C0,RADIUS,2.0
C2=CIRCLE/XSMALL,L1,XSMALL,OUT,C0,RADIUS,2.0
C3=CIRCLE/XLARGE,L1,YLARGE,IN,C0,RADIUS,2.0
C4=CIRCLE/XSMALL,L1,YLARGE,IN,C0,RADIUS,2.0
C5=CIRCLE/YLARGE,L1,XLARGE,IN,C0,RADIUS,2.0
C6=CIRCLE/YSMALL,L1,XLARGE,IN,C0,RADIUS,2.0
C7=CIRCLE/XLARGE,L1,XLARGE,OUT,C0,RADIUS,2.0
C8=CIRCLE/XSMALL,L1,YSMALL,OUT,C0,RADIUS,2.0

The directional modifiers are defined here.


Radius and Tangent to 2 Circles

CIRCLE/modifier1,modifier2,circle1,modifier3,circle1,RADIUS,radius
modifier1: XLARGE | XSMALL | YLARGE | YSMALL
modifier2: IN | OUT
modifier3: IN | OUT
The defined circle is tangent to the given circles circle1 and circle2 with the given radius.  The second and third modifiers are applied first.  Modifier IN is used if either the given circle or the defined circle is inside the other.  Otherwise modifier OUT is used.  The first modifier applies when there are 2 possible solution circles and selects the circle whose center meets the criteria when compared with the other possible solution circle.  Otherwise it is immaterial.

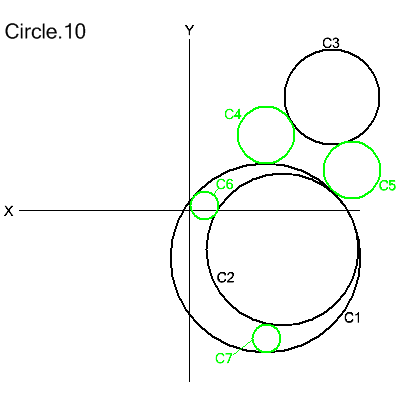
C4=CIRCLE/YLARGE,OUT,C1,OUT,C3,RADIUS,3.0
C5=CIRCLE/YSMALL,OUT,C1,OUT,C3,RADIUS,3.0
C6=CIRCLE/XSMALL,IN,C1,OUT,C2,RADIUS,1.5
C7=CIRCLE/XLARGE,IN,C1,OUT,C2,RADIUS,1.5

The directional modifiers are defined here.


Through 2 Points and the Radius

CIRCLE/modifier,point1,point2,RADIUS,radius
modifier: XLARGE | XSMALL | YLARGE | YSMALL
The defined circle passes through point1 and point2 with the given radius.  There are 2 possible solution circles and the modifier selects the circle whose center meets the criteria.


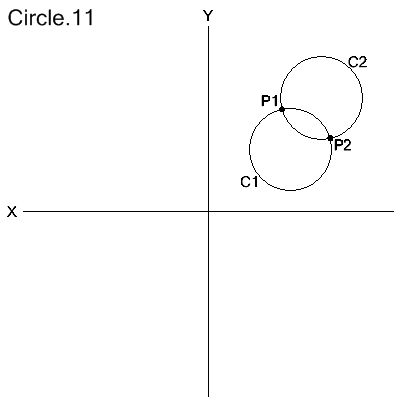
C1::CIRCLE/XSMALL,P1,P2,RADIUS,4.0
C2::CIRCLE/YLARGE,P1,P2,RADIUS,4.0

The directional modifiers are defined here.


Tangent to 3 Lines

CIRCLE/modifier1,line1,modifier2,line2,modifier3,line3
modifier1: XLARGE | XSMALL | YLARGE | YSMALL
modifier2: XLARGE | XSMALL | YLARGE | YSMALL
modifier3: XLARGE | XSMALL | YLARGE | YSMALL
The defined circle is tangent to line1, line2 and line3.  All 3 lines cannot be parallel and none can be collinear with another.  Each line is associated with the modifier which precedes it.

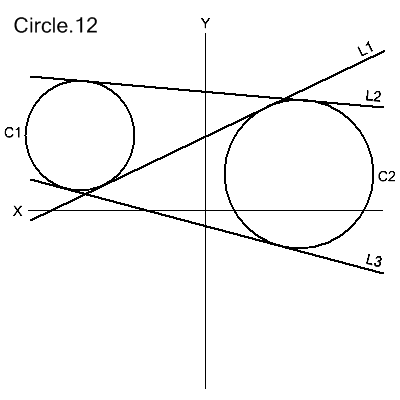
C1::CIRCLE/YLARGE,L1,XSMALL,L2,YLARGE,L3
C2::CIRCLE/YSMALL,L1,YSMALL,L2,XLARGE,L3

The directional modifiers apply to the 2 possible locations of the circle's center point.  The directional modifiers are defined here.



Tangent to 2 Lines and a Circle

CIRCLE/modifier1,TANTO,line1,modifier2,TANTO,line2,modifier3,modifier4,TANTO,circle
modifier1: XLARGE | XSMALL | YLARGE | YSMALL
modifier2: XLARGE | XSMALL | YLARGE | YSMALL
modifier3: XLARGE | XSMALL | YLARGE | YSMALL
modifier4: IN | OUT
The defined circle is tangent to lines line1 and line2 and to circle.  Modifiers 1 and 2 specify the location of the defined circle's center in relation to the given lines.  Modifier 4 specifies the location of the defined circle's center in relation to the given circle.  Modifier 3 is used as a tie-breaker in case there are 2 possible solution circles after the other modifiers are applied (see  Figure Circle.13a below).

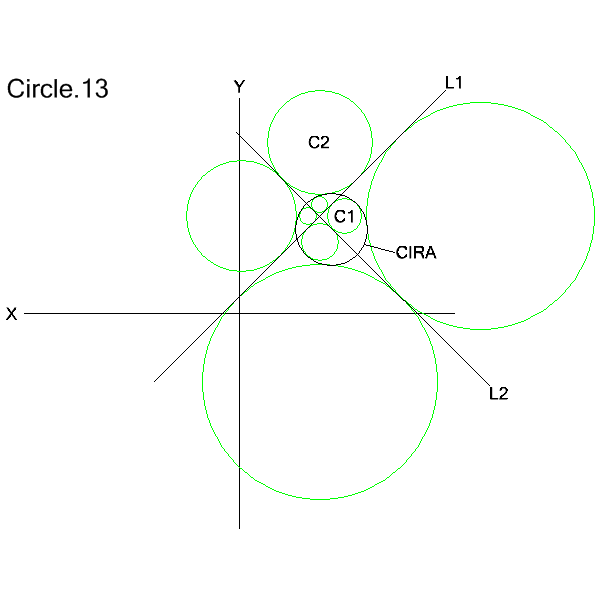
C1=CIRCLE/YSMALL,TANTO,L1,YLARGE,TANTO,L2,XLARGE,IN,TANTO,CIRA
C2=CIRCLE/YLARGE,TANTO,L1,YLARGE,TANTO,L2,YSMALL,OUT,TANTO,CIRA



Figure Circle.13a depicts 2 possible solution circles after modifiers 1, 2 and 4 have been applied.  In the figure above modifier 3 (XLARGE or XSMALL in this case) is used as a tie-breaker to select the required solution circle.  Otherwise modifier 3 is immaterial.

The directional modifiers are defined here.


Radius, a Point on the Circumference and Tangent to a Circle

CIRCLE/modifier1,modifier2,TANTO,circle,THRU,point,RADIUS,radius
modifier1: XLARGE | XSMALL | YLARGE | YSMALL
modifier2: LEFT | RIGHT
The defined circle is tangent to circle, passes through point, and has the given radius.  The modifiers are explained below.



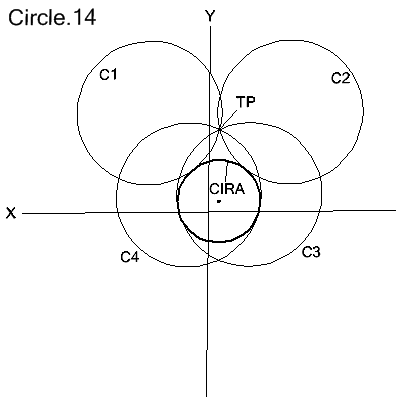
C1=CIRCLE/YLARGE,RIGHT,TANTO,CIRA,THRU,TP,RADIUS,7.0
C2=CIRCLE/XLARGE,LEFT,TANTO,CIRA,THRU,TP,RADIUS,7.0
C3=CIRCLE/XSMALL,LEFT,TANTO,CIRA,THRU,TP,RADIUS,7.0
C4=CIRCLE/YSMALL,RIGHT,TANTO,CIRA,THRU,TP,RADIUS,7.0

Modifier2 specifies the location of the center of the defined circle relative to a line passing through the point and the center of the given circle.  The sense of direction (left or right) is achieved by looking from the point toward the center of the given circle.

Modifier1 applies to the 2 possible locations of the circle's center point after Modifier2 is applied.  The directional modifiers are defined here.

A definition may have 1, 2, 3 or 4 possible solutions, depending upon the attributes provided.  The two positional modifiers are not always applicable for every definition.

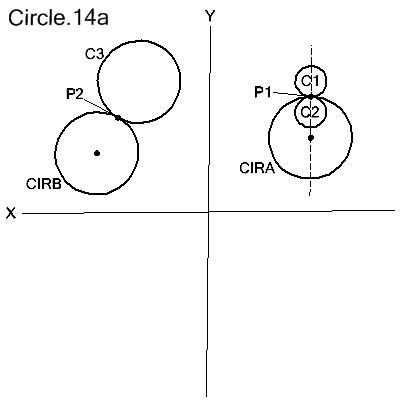
Example 1:  In figure Circle.14a below the centers of C1 and C2 lie on the line passing through P1 and the center point of CIRA.  Therefore only Modifier1 is applicable as there is no sense of left or right between the 2 possible solutions.

Example 2:  In figure Circle.14a below circles C3 and CIRB have the same radius.  Therefore there is only 1 solution and neither positional modifier is applicable.

To summarize:  If the definition has 1 possible solution then neither modifier is applicable.  If the definition has 2 possible solutions then only 1 of the modifiers is applicable.  If the definition has 3 or 4 possible solutions then both modifiers are applicable.




Intersection of a Plane and a Sphere

Not a valid APT definition.  Inclined circles resulting from this definition are for reference only.  They cannot be used by any other definitions or in any calculations.

CIRCLE/INTOF,plane,sphere
The defined circle is formed by the intersection of the given plane and sphere.



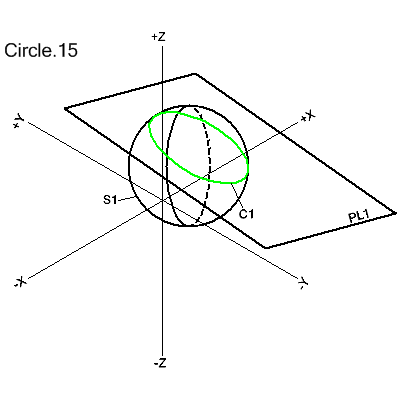
C3::CIRCLE/INTOF,PL1,S1