Shop Solver

For instructions on how to use the Define Commands, please click here.

Define Sphere

A sphere is the set of all points that are equidistant from a given point, the center.  The distance from the center to any point on the sphere is the radius.  A sphere may be defined by any of the following:

Coordinates of the Center and the Radius
Center Point and the Radius
Center Point and a Point on the Surface
Center Point and a Plane to Which it is Tangent
Passing Through 4 Points



Coordinates of the Center and the Radius

SPHERE/x-coord,y-coord,z-coord,radius
The sphere is defined with its center at the x, y, z coordinate, and by its radius.

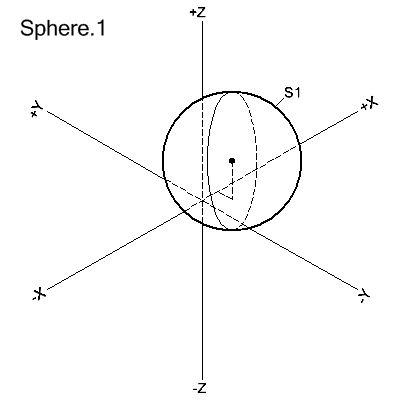
S1=SPHERE/3.0,-2.0,5.0,8.0


Center Point and the Radius

SPHERE/CENTER,point,RADIUS,radius
The sphere is defined with its center at point, and by its radius.

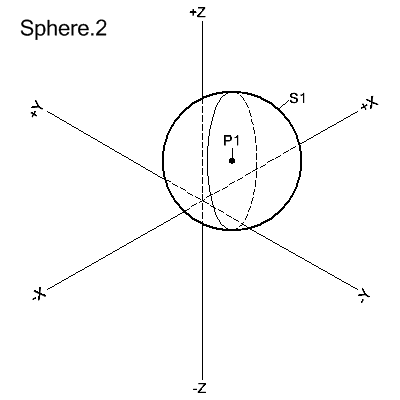
S1=SPHERE/CENTER,P1,RADIUS,8.0


Center Point and a Point on the Surface

SPHERE/CENTER,point1,point2
The sphere is defined with its center at point1.  Point2 is on the surface of the sphere.

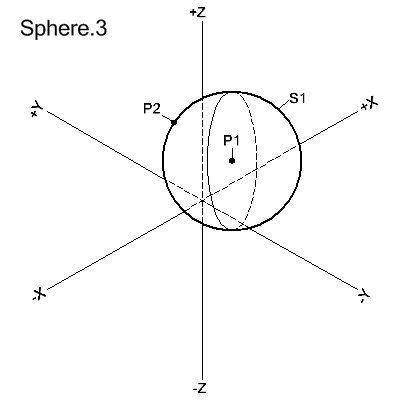
S1=SPHERE/CENTER,P1,P2


Center Point and a Plane to Which it is Tangent

SPHERE/CENTER,point,TANTO,plane
The sphere is defined with its center at point and tangent to plane.

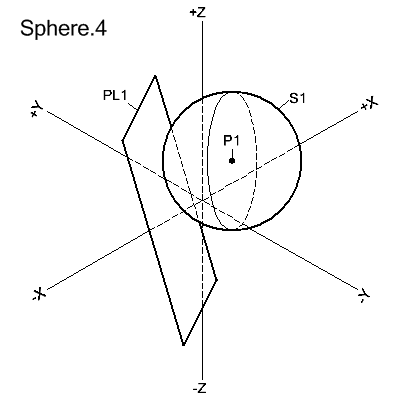
S1=SPHERE/CENTER,P1,TANTO,PL1


Passing Through 4 Points

SPHERE/point1,point2,point3,point4
The sphere is defined as passing through point1, point2, point3  and point4.  The 4 points cannot be coplanar.

S1=SPHERE/P1,P2,P3,P4