Shop Solver

For instructions on how to use the Define Commands, please click here.

Define Ellipse

An ellipse is the set of all points in a plane such that the sum of the distances from any point to the ellipse's focal points is a constant.  The perpendicular lines through the center, which intersect the ellipse at its vertices, are called the major and minor axes.  An ellipse is a circle when the length of the major and minor axes are equal.  An ellipse may be defined by the following:


Center, Semi-Major and Semi-Minor Axes, and the Angle the Major Axis Makes with the X Axis
Intersection of a Plane and a Cylinder (future)
Intersection of a Plane and a Cone (future)


Center, Semi-Major and Semi-Minor Axes, and the Angle the Major Axis Makes with the X Axis

ELLIPS/CENTER,point,length1,length2,theta
The ellipse is defined with its center at point.  Length1 is the length of the semi-major axis; length2 is the length of the semi-minor axis.  Theta is the angle of the major-axis, measured off of the X axis.

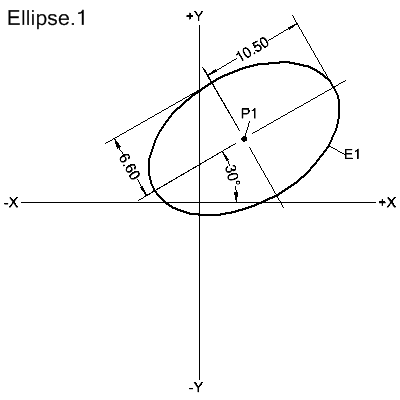
E1=ELLIPS/CENTER,P1,10.5,6.6,30.0